Introduction

In this post we’ll look at the problem of keyword matching including a number of approaches, applications and the Aho-Corasick algorithm.

Statement of problem

To begin, let’s define the keyword searching problem.

Given a list of strings \(K = [s_1, \ldots, s_n]\) (called keywords) and a (usually) much longer string \(C\) (called the corpus) count the number of times each keyword appears in the corpus.

Let \(|s_i|\) be the length of the \(i\) - th keyword and let \(m\) be the length of the corpus \(C\).

For example suppose we had \(K = [ \text{“he”}, \text{“she”}, \text{“his”}, \text{“hers”} ]\) and \(C = \text{“ushers”}\). The output of the algorithm should show that \(\text{“he”}\) occurs once, \(\text{“she”}\) occurs once, \(\text{“hers”}\) occurs once and \(\text{“his”}\) occurs zero times.

Naïve approaches

The most straightforward solution to this problem would be a brute force search overall all the keywords. For each keyword \(s_i\), we check if the substring of \(C\) starting at index \(j\) matches \(s_i\). It takes \(O(|s_i|)\) time to determine if each substring of \(C\) is equal to \(s_i\), and assuming keywords can be approximately as large as the corpus in the worst case (that is \(|s_i| \approx m\)), the overall cost of counting the number of times \(s_i\) appears in \(C\) is \(O(m^2)\). Since we repeat this search for each of the \(n\) keywords, this solution runs in \(O(n m^2)\) overall.

We can quickly improve upon this by using the Knuth–Morris–Pratt algorithm for much faster string matching per keyword. KMP simplifies the counting of each keyword to be \(O(m)\) by taking advantage of the fact that if a string has partially been matched, we may not need to check all possible starting indicies in \(C\). This reduces the total cost to \(O(nm)\) overall, already significantly than the most naïve approach.

If we think through this final solution, we should note that we can likely improve the speed of our solution by leveraging the fact that keywords often share a prefix or a suffix. For example, in the original example above, \(\text{“he”}\) and \(\text{“she”}\) share a suffix, \(\text{“he”}\) and \(\text{“hers”}\) share a prefix. Often pattern of prefix and suffix repetition occurs in practical applications since large lists of keywords that are in a language typically share linguistic roots.

Revisiting tries

A trie is a popular search tree data structure used for auto-complete and substring search among other applications. Given a set of strings (possibly keywords or suffixes of a string) the tree is grown by adding edges down from node to node where edges represent letters in each of the strings being added.

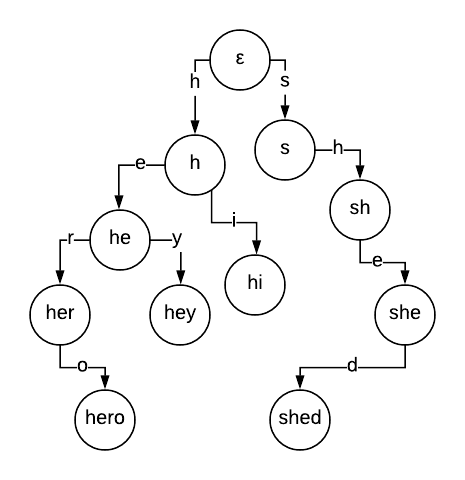
For each string we start at the top of the trie and continue either following if a node exists for the edge corresponding to the current letter or adding new nodes until each of the strings is exhausted. Searching a new string for one of the keywords is now trivial, we follow the nodes down the trie node by node using the characters in the corpus string to navigate. While at first this may seem like this is an answer to our problem, this will only find keywords that begin at the start of the corpus. For example we would find “race” in “racecar”, but we would not find “car”.

The Aho-Corasick algorithm

Building on the structure of a trie, the Aho-Corasick algorithm defines three key functions

• The goto function that determines given a current node and an input letter what node to proceed to
• The fail function that determines given a current node where to proceed if goto fails
• The output function that determines the keywords that end at a given node

What is essentially formed by the algorithm is a finite state machine. Given the three functions, we complete the following steps from starting at the root node to scan a corpus for keywords. Let the current state be denoted as \(s\),

1. Read in a new character \(a\) from the string if the corpus has not been exhausted
2. Compute goto(s, a)
3. If goto(s, a) failed, then set \(s\) to fail(s) then return to step 2
4. Set \(s\) to the value of goto(s,a)
5. If output(s) is non-empty, record the new keywords we have found
6. If the corpus has not been exhausted, return to step 1

At the conclusion of this procedure we are left with a record of each of the (possibly overlapping) keywords that were found in the corpus as well as the locations at which each keyword ended. Aho-Corasick performs best in the case that we have fixed set of keywords that we search on multiple long strings of text. If we want to add, remove or change keywords we are required to rebuild the state machine from scratch.

Building the functions

Initially, we generate a trie to form the basis of our state machine. The trie gives transitions between states for the available letters but does not guarantee there is an explicit transition from every state for each letter. For example in the above trie there is no transition from the “to” node for the letter e. In the terminology we used in the previous section, we have only defined the goto function and are now left to define the fail function.

Suppose we were searching for the keywords \(\text{“hers”}\) and \(\text{“shes”}\). The trie we have constructed will look something like this

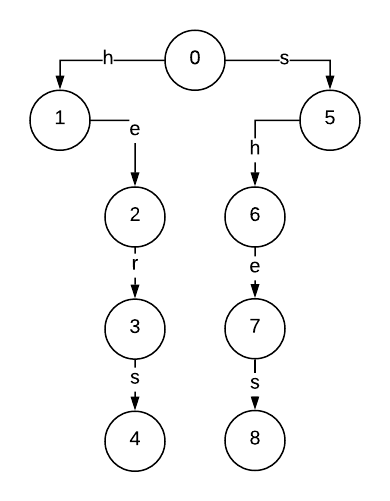
To consider what the transitions will look like for the fail function, suppose we have already read in “she” into our state machine, at which point we will be at state 7. If we read in an “s” the goto function correctly describes we should transition to state 8. However if we read in an “e” next, where should we transition? An obvious answer may be that we should return to the root, node 0, but this is not always the case. Suppose the next character read in was “r”. Instead, we would like to transition to state 3. Why is this? Well the last 4 characters we read in at this point are “sher”, and state 3 is the node we reach from tracing our “her”. However, since we already specify the transition from state 2 to state 3 (“he” \(\rightarrow\) “her”) we really are wanting fail to transition us from state 7 to state 2.

This is since state 2 corresponds to the longest proper suffix of the pattern from state 0 to state 7 that exists in our graph. We are only throwing away the “s” out of the letters we have read in so far. Throwing away the smallest prefix possible ensures that we do not miss any keywords. If instead of reading in an “r” next we had read in a “h” to get “sheh”, we would fail from state 7 to state 2, then fail again from state 2 to state 1 and finally from state 1 to state 0 since none of states 7, 2 or 1 specify a goto transition with “h”. At that point once we have “fallen back” to state 0, we move forward and consume the “h” and move to state 1.

We can construct the fail function iteratively using breadth first search to construct fail fully for each node starting at the children of the root and moving down the tree. The output function is also constructed in a similar way since each keyword may appear more than one nodes output set. For example, as we have seen “he” is a proper suffix of “she”, therefore if we reach state 7, not only have we read in “she” but also “he”!

After completing all fail transitions, we arrive at the following state machine

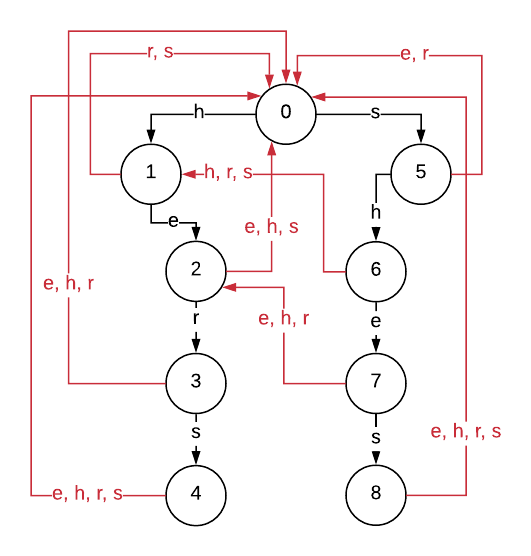
which we could use to count the frequency of the strings \(\text{“hers”}\) and \(\text{“shes”}\) in strings.

Implementation

You can find an example implementation here in Python with some tests. We represent the goto function as a list of defaultdict objects. In this representation goto(s,a) is computed by self.goto[s][a]. The fail function is represented as a list and fail(s) is simply the entry self.fail[s]. Finally the output function is represented as a list of set objects where as expected self.output[s] will return the set of keywords that end at a particular node.

Applications

Fast keyword matching has a number of very practical use cases beyond Computer Science textbooks.

Last month Lewis Van Winkle discussed F5Bot, a free service that emails users when selected keywords are mentioned on Reddit or Hacker News, in a blog post here. With the Aho-Corasick algorithm, F5Bot is able to scan through all posts and comments on Reddit and Hacker News in real-time while running on a (tiny VPS). At peak rates, Lewis notes this reaches approximately 50 posts per second scanning approximately 5000 keywords.

Another popular example is the scanning of news articles for references to companies by hedge funds and quantitative trading firms. The most public example of this is known as the Hathaway Effect, coined by Dan Mirvish here published in the Huffington Post. The article documents the tendency for news articles relating to Anne Hathaway to be correlated with positive returns in $BRK.A. The most popular explanation for this effect is hedge fund bots scanning through news articles mistaking the actress for news about Berkshire-Hathaway. The Aho-Corasick would be a very attractive algorithm to use in this circumstance since we have a relatively fixed set of keywords (names of SP500 companies) and multiple long strings (news articles) as mentioned earlier.

References

Alfred V. Aho and Margaret J. Corasick. 1975. Efficient string matching: an aid to bibliographic search. Commun. ACM 18, 6 (June 1975), 333-340. DOI=http://dx.doi.org/10.1145/360825.360855